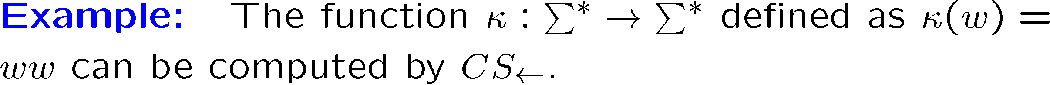Chapter 4 Turing Machine
图灵机定义
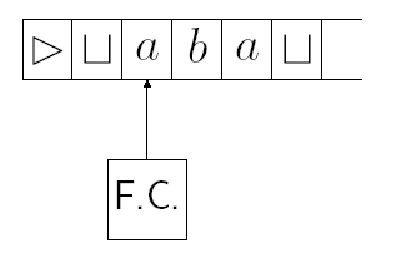
- head 可以读写,左右都可以移动
- tape 无限长度
正规定义:

halting state 是停机状态,左右箭头就是指,输入了这个符号,将导致状态转移,并且读写头进行相应的一次移动
注意,由于只有左边有 end,右边是无限大的,在右边一定会出现无穷多个连续的 空格
[!EXAMPLE]
[!EXAMPLE] 永不停机的情况
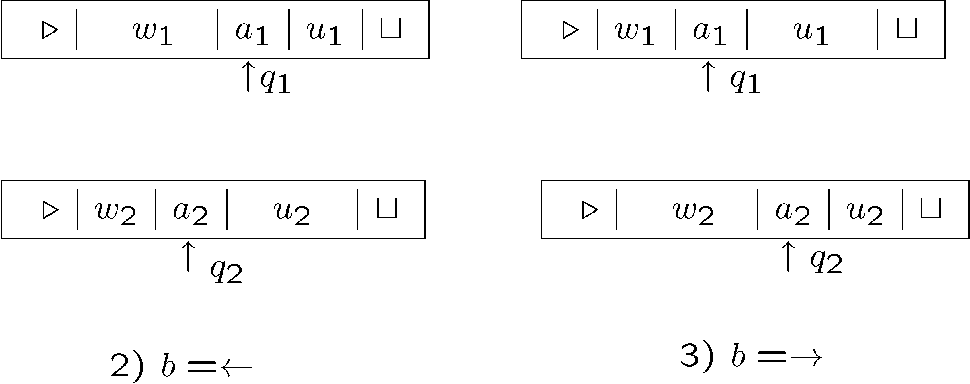
图灵机格局(configuration)
格局是给图灵机照一个 快照,用来描述图灵机运行到某一时刻是什么情况的
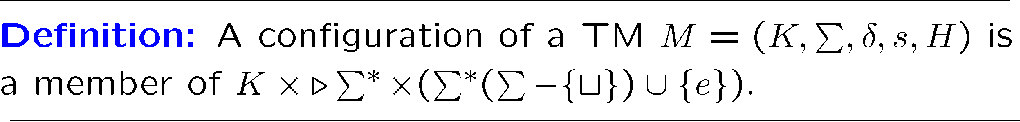
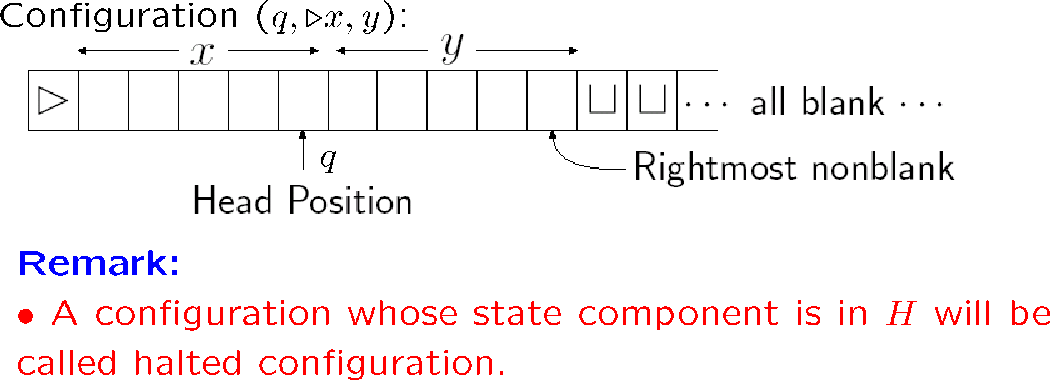
[!EXAMPLE]
注意怎么描述,主要是目前所在状态左边都要记录,右边如果全是空就不用记录,否则也要记录
符号底下放一个横线表示读写头的位置
计算(设计)图灵机(computation)

上面这些是显然的,但是要看懂这种专业的描述
[!EXAMPLE]

基本图灵机
我们接下来希望用最简单的图灵机构成更复杂的图灵机
Basic Machines 的定义:
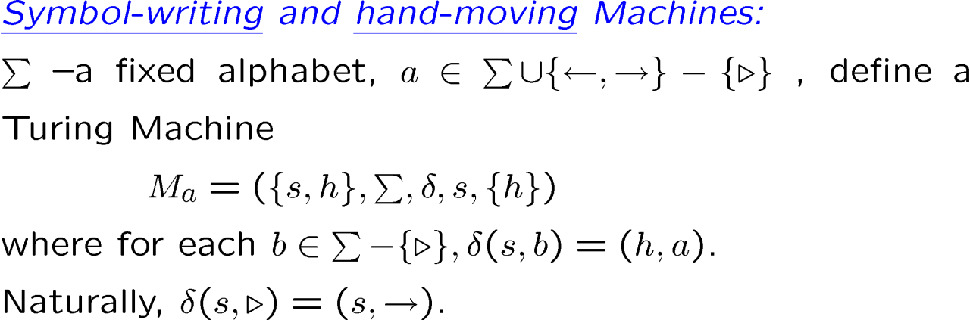
缩写:我们可以用 a 表示 Ma,L 表示 M←,R 表示 M→
下面我们用这个 Basic Machines 搭建更复杂的图灵机
图灵机构建规则如下:

也就是说,我们想组装三个图灵机到一起,就选取其中一个为起始机器,然后在其终止状态处进行机器切换
[!NOTE]
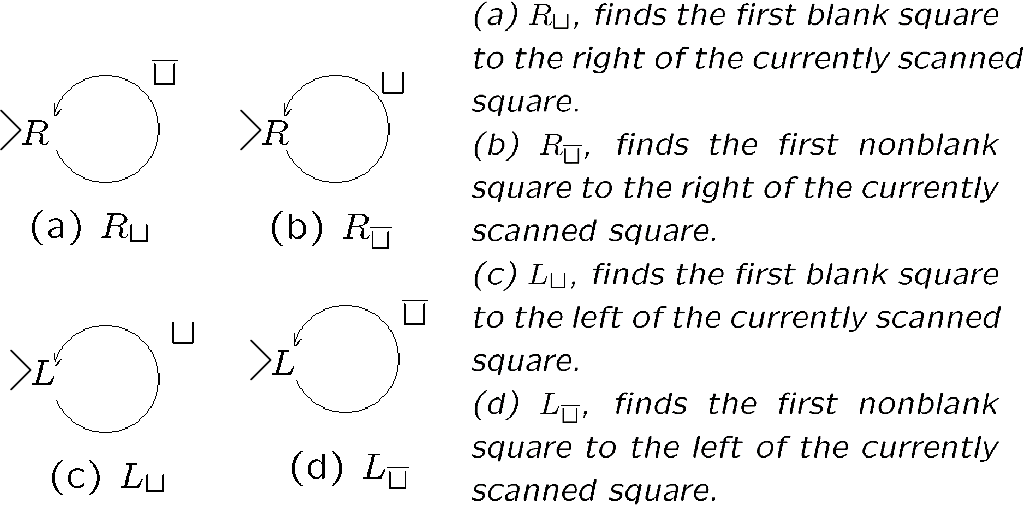
一些常见的基础图灵机及其含义
下面几个图灵机可以连续向左/向右找出第一个空格/非空格元素
[!EXAMPLE]
注意看横线是在空格的上面还是下面
用图灵机进行计算
判定问题的计算
[!EXAMPLE]
我们将图灵机稍微修改一下,只修改里面的 \(H\),一个符号表示 yes,另一个表示 no,含义显而易见

语言如何被判定

[!EXAMPLE] 一个语言如何被判定
书上的是有问题的?(abc)^n 也会被接收

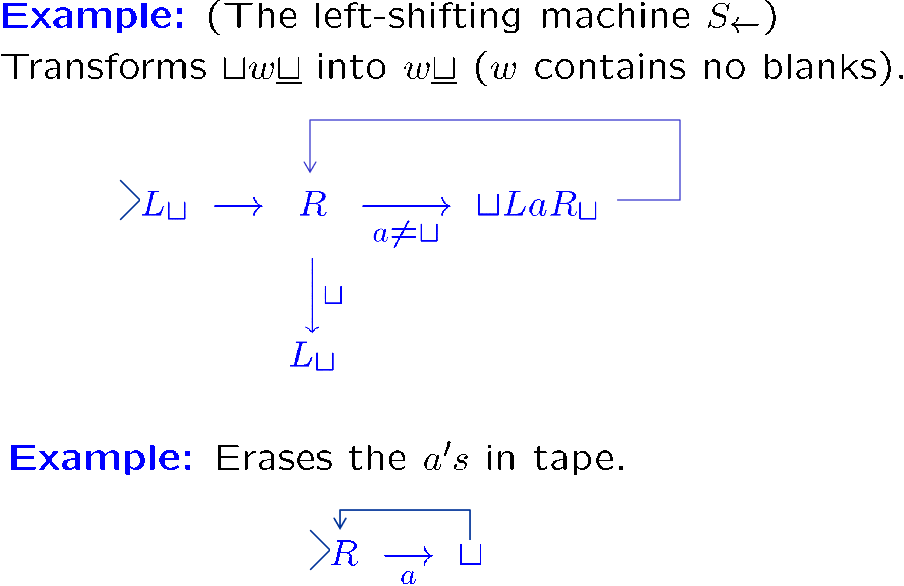
计算函数


[!EXAMPLE]
C 和 S→ 是之前例子里的拷贝机器和左移机器
递归函数
我们上面的函数其实还是字符串函数,但我们平时用的更多是数值函数
这个问题简单,在字符串函数和数值函数之间构建一个映射即可,将数值转化为二进制数字符串
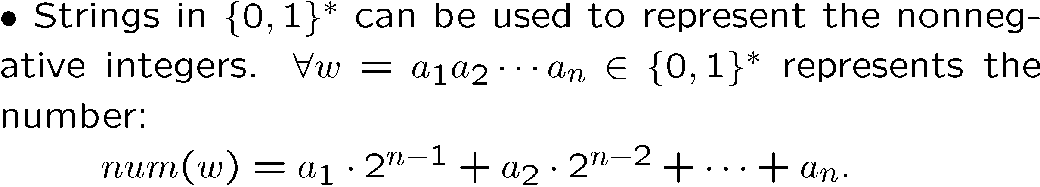
接收二进制数字符串的图灵机:
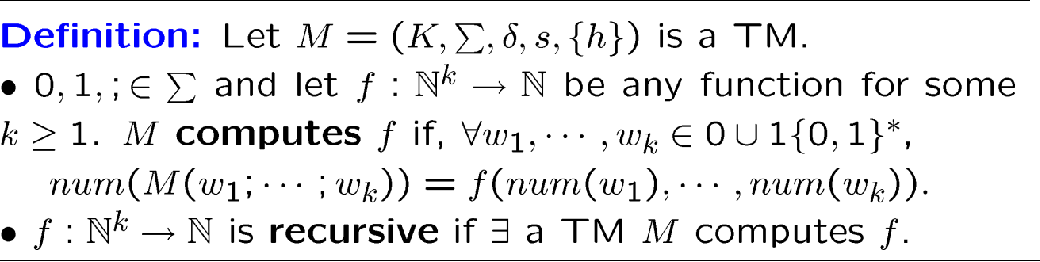

[!EXAMPLE]
递归可枚举语言/半判定语言
递归语言就是完全判定语言,可以判定是 yes 还是 no
半判定语言可以判定是 yes,但无法判定是 no
什么是递归可枚举语言:

注意是充要条件,也就是说,不属于 递归可枚举语言 的字符串无法使图灵机停下来

这里我们定义了一个新的符号来标记一个字符串是否属于递归可枚举语言
[!EXAMPLE]
一些性质
- 递归语言的补集也是递归语言
补集就是把 yes 和 no 换一样

- 递归语言一定是递归可枚举语言
就把 no 从 H 中移除即可
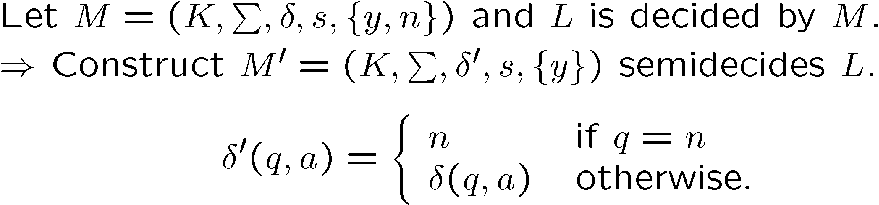
- 两个递归语言的 交集 和 并集 都是递归语言
废话,结果依旧能被两个图灵机判定