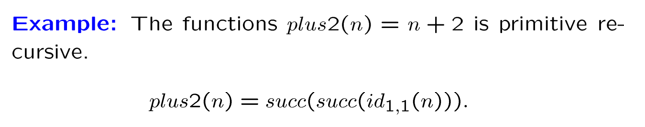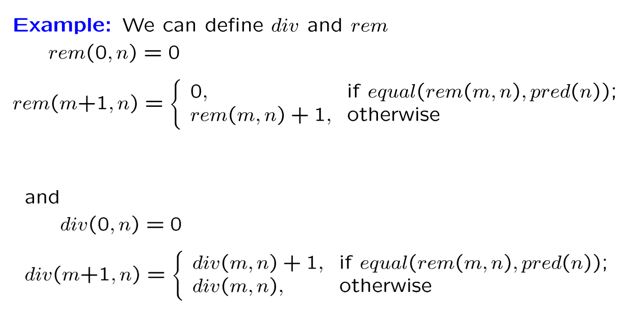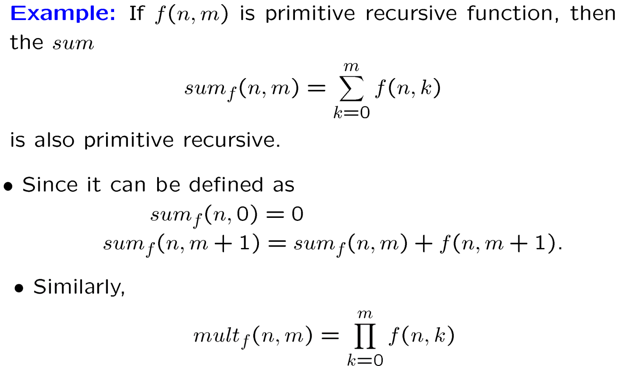4.1 文法 & Numerical Functions
图灵机的拓展
我们可以增加图灵机的配置使其效率更高
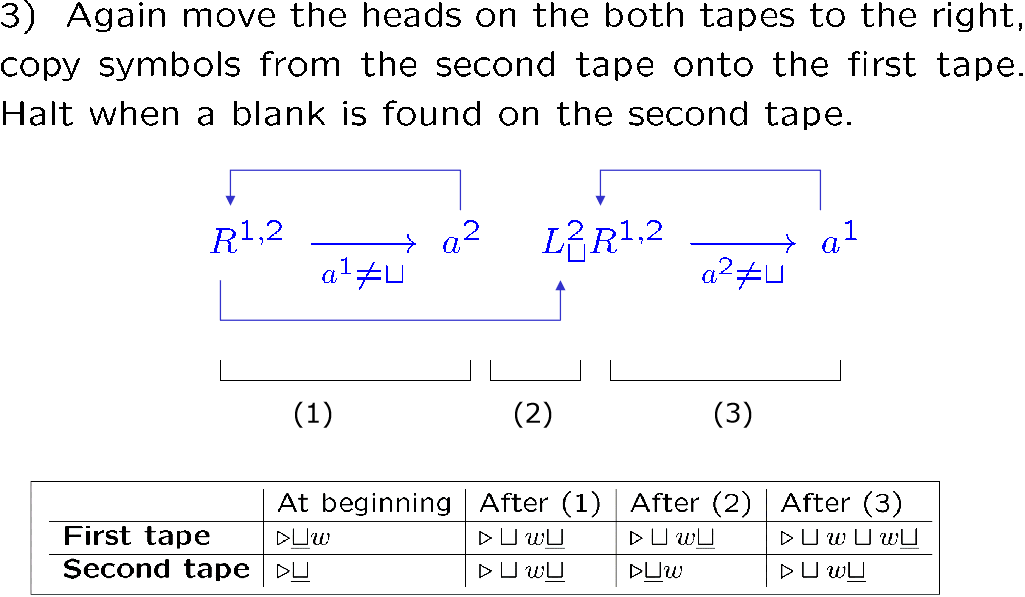
Multiple tape

同时读入每个带的内容,同时对每个带进行操作
它的格局就得把每条带的内容都写上
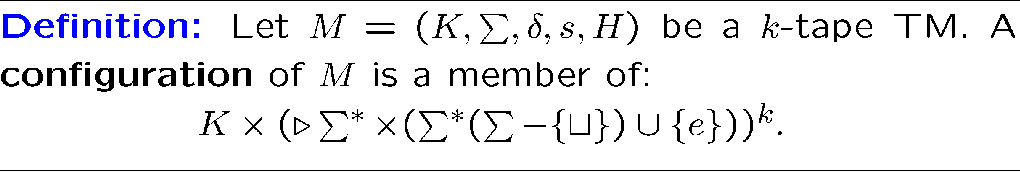
我们要求输入的字符串只能放在第一条带,其它带初始是空的,但都有自己的读写头
最后的输出也只有第一条带,其它带被忽略
[!EXAMPLE]
多带图灵机 和 标准图灵机 是等价的

证明: PPT 44 页

单带图灵机是多带图灵机的特例,所以我们只需要证明多带图灵机能做的,单带图灵机也能做
Two-way infinite tape
即两端没有 end
Multiple head
..... 这部分看 PPT 吧
非确定性图灵机 NTM

就是原本的转移函数变成了转移关系
NTM 如何判定语言、计算函数
判定语言就只要存在一种转移路径能到达终止状态即可


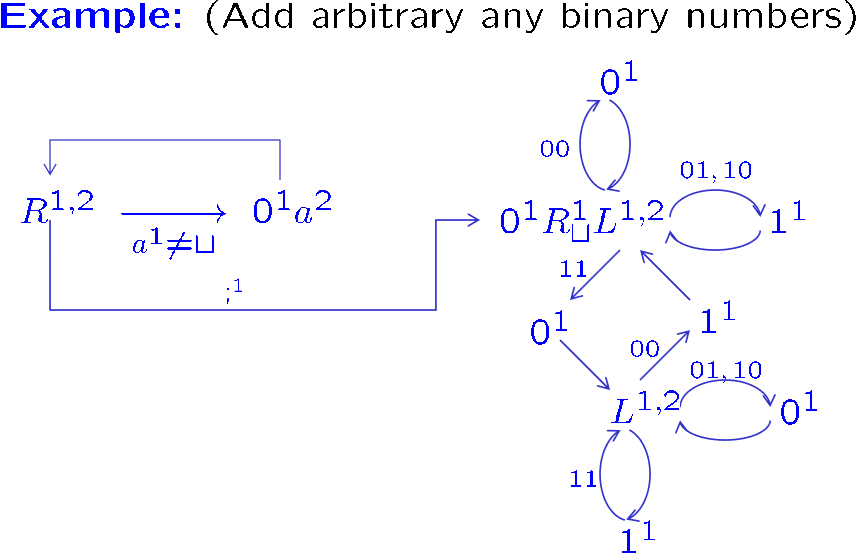
[!EXAMPLE]
NTM 与 标准 TM 的等价问题
在半判定问题上,NTM 与 TM 是等价的

[!PROOF]
PPT 61 页,证明比较难
文法(无限制文法的简称)
[!IMPORTANT]
Grammar,文法,默认指无限制文法!!!
机器的能力增强后,我们开始从 CFG 进一步拓展至无限制文法
无限制文法的定义

关键是最后一行,推导关系的左边可以有上下文也可以没有上下文
这里我们要区分上下文有关的推导与上下文无关的推导的符号:
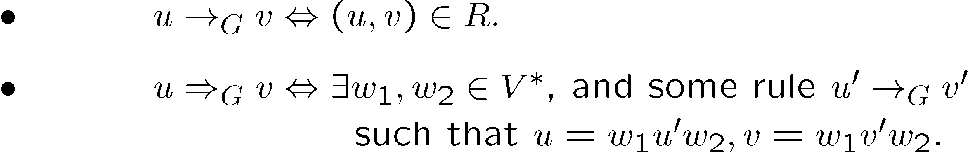
[!EXAMPLE]
[!NOTE]
可以被文法生成 等价于 属于递归可枚举
证明见 PPT 76 页,以及,82~83 页都没讲
Numerical Functions
PPL 和计算理论一起攻击我
basic functions & operations
原始递归函数类似 FA,可以从最基本的函数计算得到
有三个最原始的函数:projection functions, zero function, successor funciotn

identity function 是恒等函数,也就是投影函数,从 \(k\) 个元素值选取出某一个元素
还有两个基本运算:composition 和 recurse

primitive recursive functions
我们定义原始递归函数是通过原始函数通过拼接、递归的到的函数:

[!EXAMPLE] 证明一个函数是原始递归的
[!EXAMPLE] 加、乘、幂函数是原始递归的
[!EXAMPLE] 常量函数是原始递归的
[!EXAMPLE] 非负数取值函数是原始递归的
引入了一个前驱函数
primitive recursive predicate
原始递归谓词指只输出 0 或 1 的函数,也就是一些做判断的函数
[!EXAMPLE] 常见的原始递归谓词
原始递归谓词 的 否定 negation 还是原始递归谓词

原始递归谓词的合取和析取都还是原始递归的


[!EXAMPLE] 除法、取余是原始递归的
[!EXAMPLE] 不知道什么函数是原始递归的
[!EXAMPLE] 求和函数是原始递归的
[!EXAMPLE]

[!EXAMPLE] 存在可以计算的,但不是原始递归的函数
确切说,原始递归函数只是递归函数的一个真子集
Minimalization 极小化
我们定义一个函数的极小化如下:

即,将原函数最后一个参数设置为常数 m,如果存在一个 m,无论其它参数怎么改变,函数的值都为 1,那么,原函数的极小化函数中,这前面 k 个参数带入的结果就是 m,找不到就为 0
只要能找到一个这样的 m,那么原函数就是可极小化的:

\(\mu\) 递归
一个函数是 \(\mu\) 递归的,如果这个函数可以从基本函数出发,经过 组合、递归、可极小化函数的极小化 三种操作得到

[!EXAMPLE]
向上的箭头可以看成(m+2)^p
\(\mu\) 递归就是递归的
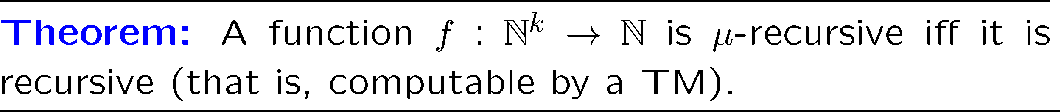
因为产生 \(\mu\) 递归的三种操作都可以分别用图灵机表示出来,所以可以设计出对应的图灵机
反过来的证明见 PPT 105 页,了解即可