Skip to content

Chapter 5 Undecidability

:material-circle-edit-outline: 约 557 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

不可判定性

PPT 计算理论（本）2024-12-16 第 1-2 节

图灵机是串行计算下最极限的计算模型

image-20241221111543510

Church-Turing thesis

任何可被“有效计算”的问题都可以由图灵机来计算

注意：

  1. Church-Turing thesis 无法被证明，不是 theorem，是假设，可能被推翻
  2. 一个算法被定义为一个总能停止（halt）且能返回正确答案的程序
  3. 一个问题是递归的，则是可判定的；否则是不可判定的
    • 即，存在一个算法能够在有限时间内确定地解决这个问题

Universal Turing Machine

纯净版的图灵机是不可编程的一小块硬件，设计好后只能解决某个特定问题

我们希望设计出一个能够解决任意问题的图灵机，即通用图灵机

将图灵机转化为编码

基本思想：将图灵机的各部件进行编码，这样就可以编程了

image-20241221113324384

上面我们确定了编码长度，编码了字符表里的所有符号以及额外的左移右移两个符号，并将四个特殊符号编在最低的位置

下面编码所有的状态，并将起始状态编在最小的位置

image-20241221113334643

最后我们把转移方程里的符号全替换为编码，我们就把整个图灵机转化为了一串字符串

[!EXAMPLE] 将图灵机编码

image-20241221113344625

image-20241221113351303

通用图灵机的表示

我们用 \(U\) 表示通用图灵机，其有如下性质

image-20241221175129334

输入机器的编码 "M" 以及初始值的编码 "w"，将输出 w 输入 M 会得到的值的编码 "x"

image-20241221175903862

通用图灵机的计算

\(U\) 需要三条 tape，用途如下：

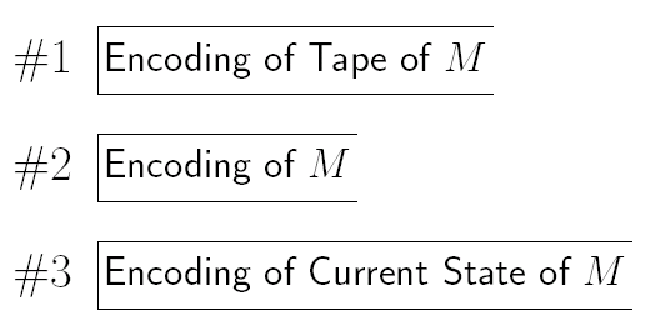
image-20241221175826553

计算步骤：

  1. 将 "M" 拷贝到第二条带，并将 "w" 左移至顶，再将 "s" 写到第三条带
  2. 我们要模拟 M 的一次计算，方法为第一条和第三条带查询第二条带上 M 的编码（实际就是转移关系的编码）相应地修改第一条带和第三条带的值
  3. 重复步骤 2，知道第三条带出现 "h"（halt 状态），当然可以不会 halt

The Halting Problem

PPT 19 页

image-20241221204457596

image-20241221204721384

image-20241221204742492