Skip to content

Finite Automata

:material-circle-edit-outline: 约 1659 个字 :material-clock-time-two-outline: 预计阅读时间 6 分钟

Deterministic Finite Automata(DFA)

确定性是指每一步的状态转移是确定的，有限是指状态是有限的

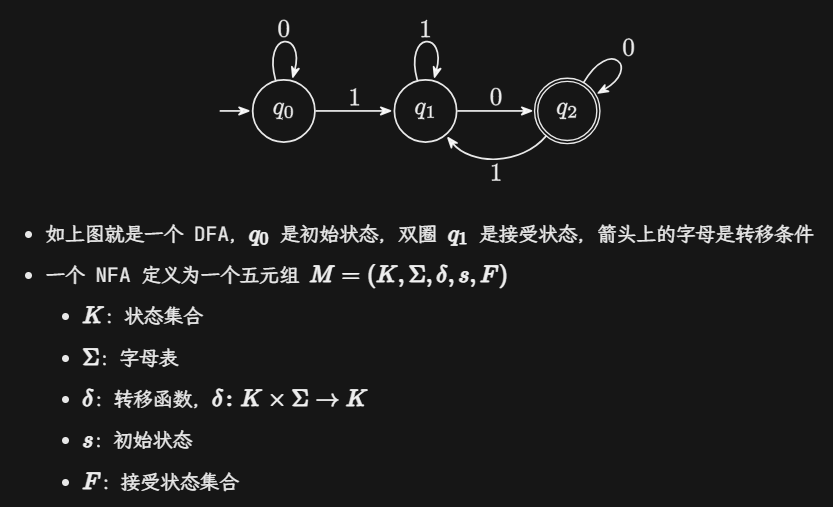
image-20241231101508677

有一个输入带，只能读，读取头只能向右移，每次只读一格，读到一个字符就改变状态

执行逻辑：输入一个字符串，从初始状态，每次取出第一个字符，根据当前状态和字符查找转移函数，得到下一个状态，直到字符串为空

configuration: \(K\times \Sigma^*\)，(q, w)，表示当前状态 q 和剩余字符串 w

\(L(M)\) 即一个状态机能接受的所有字符串的集合

语言、自动机与正则表达式 - 鹤翔万里的笔记本

NFA 可以有 e-transition，即不消耗字符的转移

NFA 接受语言需要深度遍历整棵树，而 DFA 类似 BFS 找一个叶子

NFA 虽然看起来比 DFA 强大，但其二者实际上是等价的

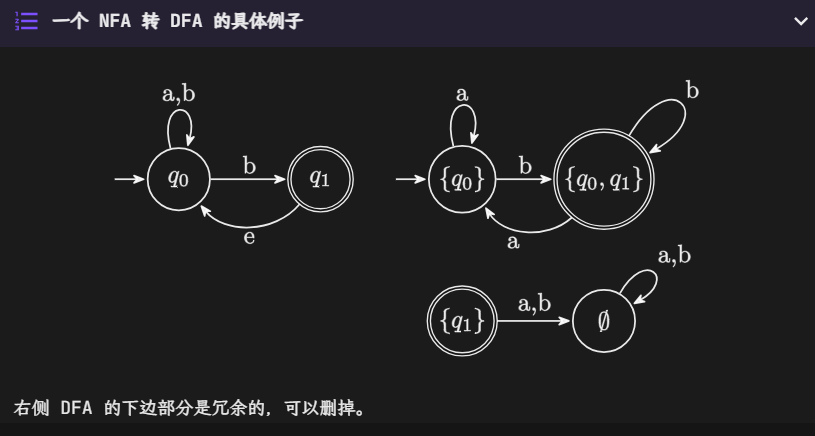
NFA 转 DFA 主要思路

  • NFA 接收一个字符，会有多个转移方案，所有可达的下一状态合在一起的集合构成 DFA 的一个状态
    • 即 DFA 的状态是 NFA 的状态的幂集，结束状态是包含 NFA 的结束状态的 DFA 状态
  • e-transition 也要考虑，且不算在字符数里

image-20241231102025589

DFA 与 NFA 的等价与转换

两个 FA 等价，当且仅当 \(L(M)\) 相等

NFA 转化为 DFA

\(E(q)\) 表达的是一个状态只接受有限个 \(e\) 能转移到的所有状态集合，注意可以多步寻找，深度搜索

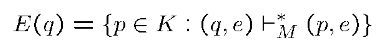
image-20241231104336206

由 NFA 构建等价 DFA

记 \(M^\prime=(K^\prime,\Sigma ,\delta,s^\prime,F^\prime)\) 为 DFA，\(M=(K,\Sigma ,\Delta,s,F)\) 为 NFA，他们是等价的

则：

  • \(K^\prime=2^K\)
  • \(s^\prime=E(s)\)
  • \(F^\prime=\{Q|Q\subseteq K,Q\cap F\neq\empty\}\)
  • 转移方程：

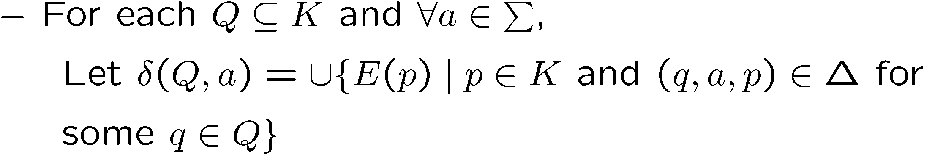
image-20241014104223738

也就是说，我们取 NFA 状态的集合作为 DFA 的一个状态

对于 NFA 所有可能的状态集合，其转移方程为，集合内所有状态的转移关系的结果的 E()

从 \(s^\prime=E(s)\) 往后推即可

注意转换后的 DFA 状态都是 集合，是 NFA 状态的集合

image-20241231105850436

FA 与 正则表达式

FA 和正则表达式是等价的：

  • 一个语言是正则的，当且仅当其可以被一个 FA 接收；
    • 即任意正则表达式均可被某个 FA 接受
  • 可被 FA 接收的语言都可以被正则表达式表达
    • 即任意 FA 均有 \(L(M) = L(R)\)

有限语言等价于正则语言

有限封闭性

能被 FA 接受的语言，基于下面五个运算符是封闭的（前提是有限次运算）

image-20241014112131511

image-20241014112512629

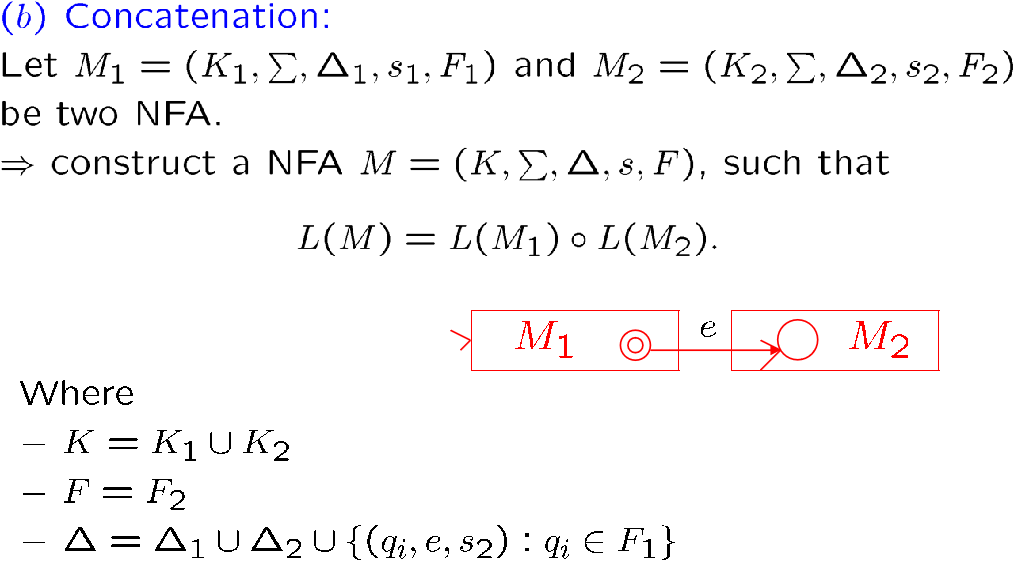
image-20241014112557669

image-20241014112648594

image-20241014112745229

image-20241014112804582

\(L(M)\) 实际上就是 FA 起始状态到终点状态的所有有向道路

我们定义字符串集合 \(R(i,j,k)\)，其元素能够从 \(q_i\) 走到 \(q_j\)，且经过的中间状态的最大下标为 \(k\)

显然这个 \(R\) 包含所有起始状态到终点状态的有向道路

然后我们证明这个是一个正则语言，思路就是 k = 0 时用正则表达式表示这个集合，然后证明对于每一个 k 都能类似地表示

image-20241016092958791

求一个 FA 能接受的语言，只需要一步一步求 \(R(i,j,k)\)，为了方便，我们可以每求一轮就把对应的 \(q_k\) 删掉

判断一个语言是不是正则的

证明正则性的思路

  • 构建正则表达式来生成这个语言（封闭性）
  • 构建一个能接受其的 FA （正则与 FA 等价）

证明正则性的思路

  • 使用泵定理

泵定理

FA 是有限机，无法处理数量不确定的（无周期性的）语言，即带有无界限变量的语言，例如 \(a^nb^n,n>0\)

也就是说，FA 处理的都是有周期性的语言（或只有一个周期的语言）

泵定理就是，\(L\) 如果是正则语言，那么存在 \(n\)，任意长度 \(\ge n\) 的字符串都可以写成 \(xyz\)

其中 \(y\ne e\)，\(xy\) 长度 \(\le n\) ，\(xy^iz\) 属于 \(L\)

image-20241016100235793

证明很简单，注意条件是 \(\omega\) 长度 \(\ge n\) ，故一定会经过 n+1 个状态，其中至少一次重复经过同一个状态，由此可以构建对应的 \(x,y,z\)

image-20241016100456318

用泵定理证明非正则语言思路如下：

  1. 假设 \(L\) 是正则的
  2. 设计出一个属于 \(L\) 的字符串 \(s\)，长度大于 \(n\)
  3. 利用泵定理得到另一个不属于 \(L\) 的字符串

利用封闭性的思路：

  1. 找出另一个正则的语言 \(L_2\)
  2. 假设 \(L_1\) 正则，那么 \(L_1\cup L_2\) 也正则，我们证明其不正则即可
  3. 当然，其它四个封闭的操作也可以

最少状态数的 DFA State Minimization

对于某个 DFA，我们尝试找一个等价的 DFA，让其拥有最少的状态数

两个等价的方法：

  1. 移出所有不可达状态
  2. 找出所有可到达状态

后者更简单，算法如下：

image-20241021193800546

再将等价的状态进行合并

状态等价就是在这个状态上，输入相同的字符能得到同样的结果

字符串等价就是输入后能得到相同末状态

关于语言等价的等价类

等价有三个特性，自反，对称，传递，满足的话就是等价

基于语言的等价关系

\(x\approx_Ly\) 表示：

对于任意 \(z\in \Sigma^*\)，如果 \(xz\in L\)，则 \(yz\in L\)，如果前者不属于，后者也不属于

基于此我们可以划分等价类：

image-20241021083630255

基于 DFA 的等价关系

\(x\sim_M y\) 表示：他们输入 M 会转移到相同的状态

我们定义 \(E_q\) 表示所有会停在 \(q\) 上的字符串，则可划分等价类：

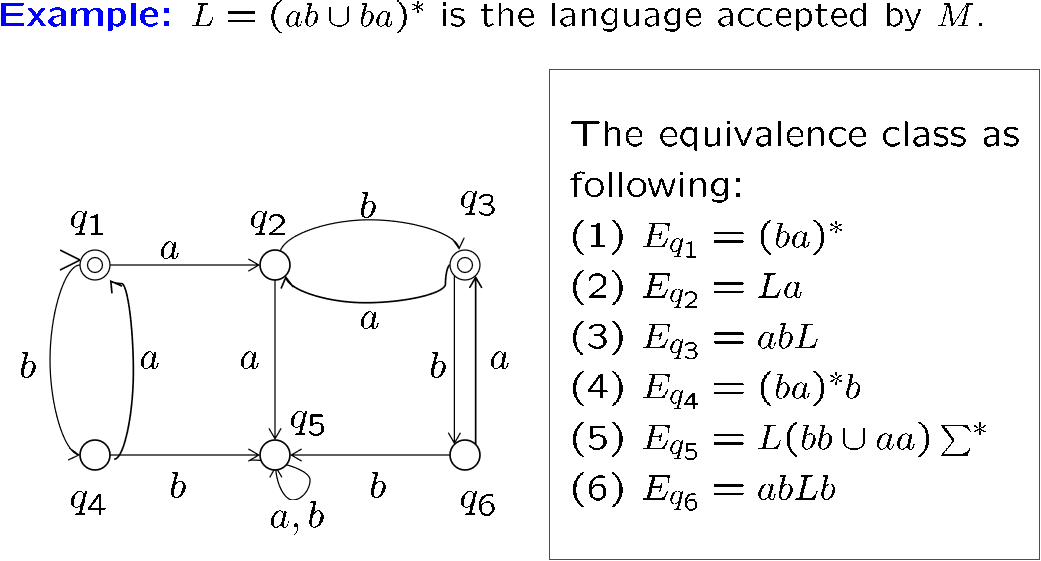
image-20241021084448268

两种等价关系的联系

机器等价类更细，是在语言等价类上进一步划分的

如果 \(x\sim_M y\)，则 \(x\approx_Ly\)，但是不能反过来

image-20241021084655145

image-20241021085355919

refinement 即细分，前者划分地更细，而且是在后者的基础上进行划分的

image-20241021201402781

Myhill-Nerode 定理

\(L\) 是正则的，当且仅当 \(\approx_L\) 等价类是有限多的

可以用来证明非正则语言

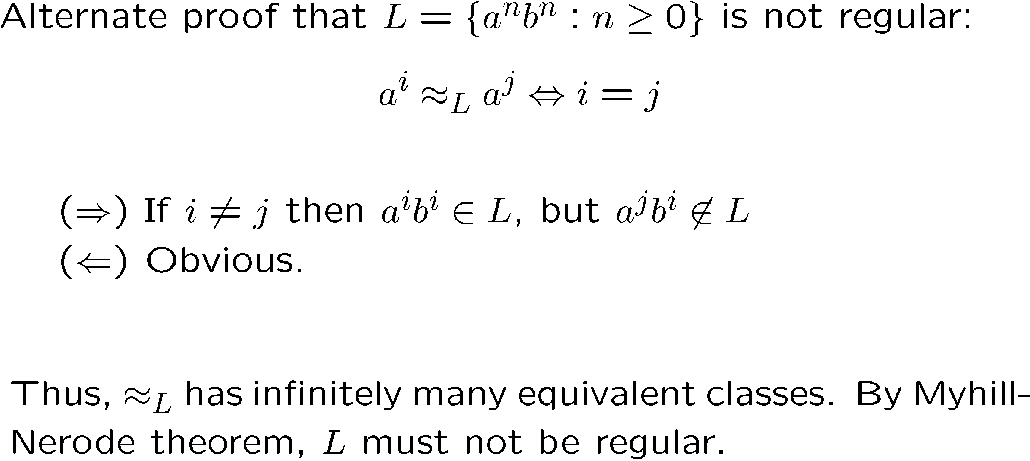
image-20241025111519466

FA 最小化算法*

两个状态等价的意思是，对任意字符串，要么都是能进入终止状态，要么都不是

求解最小化 DFA 的过程就是一步步合并等价状态的过程

编译原理学习笔记（十五）~最小化 DFA_dfa 最小化-CSDN 博客

里面的可区分就是不等价