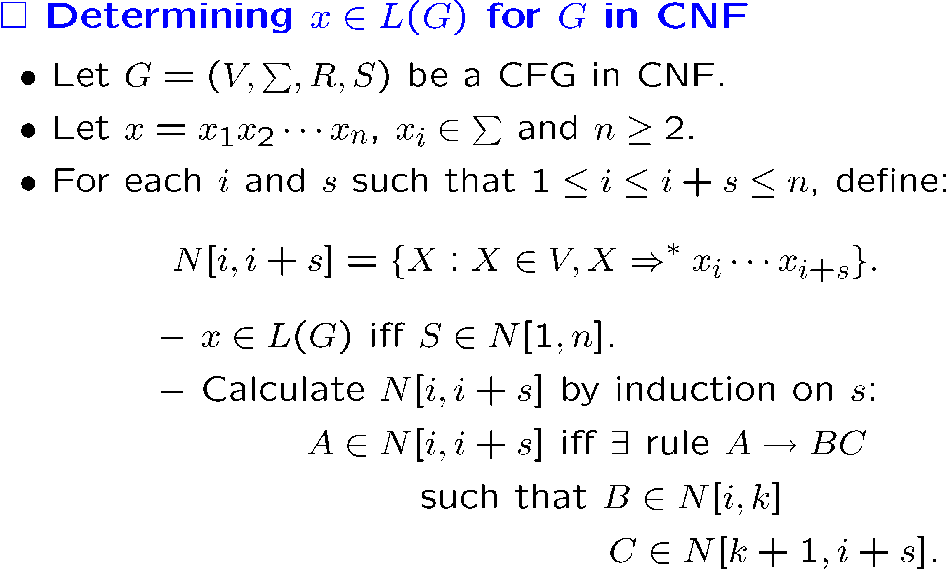Skip to content

Context-Free Language

:material-circle-edit-outline: 约 1003 个字 :material-clock-time-two-outline: 预计阅读时间 3 分钟

image-20241028091420312

CFGrammer 定义

image-20241231141839662

\(L(G)\) 是能通过 \(G\) 生成的所有语言的集合

\(L\) 是一个 context-free language（CFL），当且仅当 \(\exist\) 一个 CFG \(G\)，\(L=L(G)\)

[!NOTE]

证明一个语言是上下文无关的，就是要写出能生成其的 CFG

所有正则语言都是 CFL，我们可以直接构造出 DFA 对应的 CFG，只需要把 DFA 每条边进行一定的描述，就得到了对应的上下文无关文法

image-20241124221559314

Chomsky Normal Form

后面判断字符串能否被 CFG 生成会用到

一个 CFG 是 Chomsky Normal Form（CNF），如果它的所有规则都是以下三种形式之一

  • \(S → e\)：只有起始符号可以推导出空串
  • 不能生成空串
    • 这类语法生成的字符串长度不会小于 2
  • \(A→BC\) for some \(B, C∈V−Σ\), ：非终结符号可以推导出两个非终结符号
  • \(A→a\) for some \(a∈Σ\) ：非终结符号可以推导出一个终结符号

特点：生成一个长度为 \(n\) 的串需要 \(2n−1\) 步推导

定理：任何一个 CFG 都可以转换成等价 CNF 形式（即保证生成语言相同）

将 CFG 转化为 CNF

后者的 \(L(G)\) 只比前者少了空字符串和长度为 1 的字符串

image-20241231142420906

第一步，处理长规则

就是拆分成多个长度为 1 的短规则，留到第三步继续处理

对应上面的规则 4

image-20241130103417717

第二步，处理空规则

先把所有可能生成 \(e\) 的规则放入一个集合

对应上面的规则 2，不一样的地方是，要保留原来的

image-20241130103509652

第三步，处理短规则

对应上面的规则 3

image-20241130103553059

image-20241130103556700

？？？？？？第三步哪来的，不懂

应该是，如果右边为终结符，就检查其它规则，如果有 \(S_1\) ，复制一份该规则并替换

Pushdown Automata

下推自动机（Pushdown Automata, PDA）是 NFA 的一个扩展，是非确定性的

在 NFA 基础上加了一个额外的栈结构，并在状态转移时会进行栈操作

PDA 和 CFG 等价

image-20241231145841719

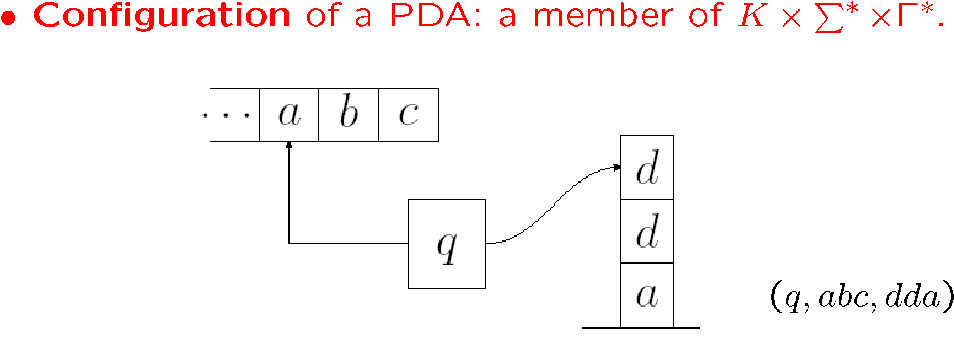
image-20241124232048993

如果一个字符串输入给 PDA 能得到：字符串被消耗完，stack 清空，到达结束状态

那就说 PDA 接受这个字符串

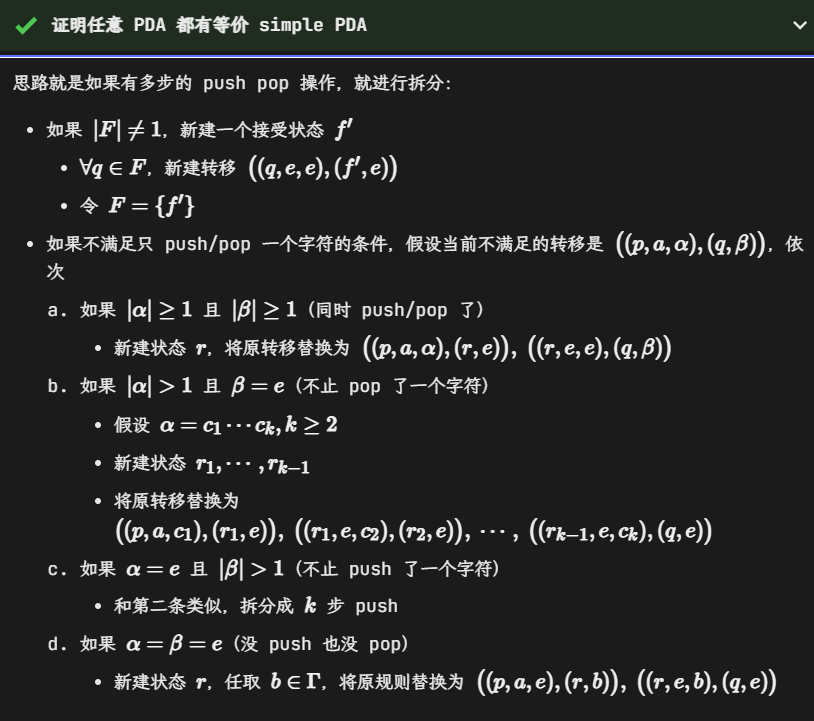
Simple PDA

image-20241231145936677

任意 PDA 都有等价的 Simple PDA

image-20241125130859278

注意 \(\Gamma\) 是字母集合，所以这里是指 \(\beta\) 只能有一个字符，即 stack 读只能读一个字符

写 stack 的时候（即替换）最多只能写两个字符

？？？？？矛盾？

image-20241231145955890

PDA 与 CFG 等价

根据 CFG 构造 PDA

对于 CFG 生成的 CFL，我们就设计一个可以接收其 leftmost derivation 的 PDA

设计如下，注意这里 PDA 的 \(\Sigma\) 就是 CFG 的终结符集合

image-20241125124125875

只需要两个状态，三个转移关系：

  1. 把起始符压入栈
  2. 把 stack top 进行规则替换
  3. stack top 是终结符时可以 pop
    • 因为只有非终结符可以进行替换

根据 PDA 构造 CFG

把 “读很长的字符串” 这个动作分解为很多个 “读一个个字符” 动作

待分解的 PDA 定义如下：

image-20241125131432147

先将读进行分解：

image-20241125154345377

再将写进行分解：

image-20241125154416207

特别的，输入 \(e\) 时，我们依旧要保证输入的是一个字符，所以我们从 stack 借一个字符，拿出来后再写进去：

image-20241125154443226

最后我们根据上面得到的 simple PDA，构造一个对应的 CFG：

image-20241125160026112

第一处的小 s 少了个撇

CFL 性质

Closure Properties

PDA 可以定义一个 CFL，所以根据 PDA 的结构，CFL 有以下性质：

image-20241231151357327

image-20241125160723693

image-20241125160728612

我们可以确定，CFL 与正则语言的交集是 CFL，直接把 PDA 和 DFA 并行就行了：

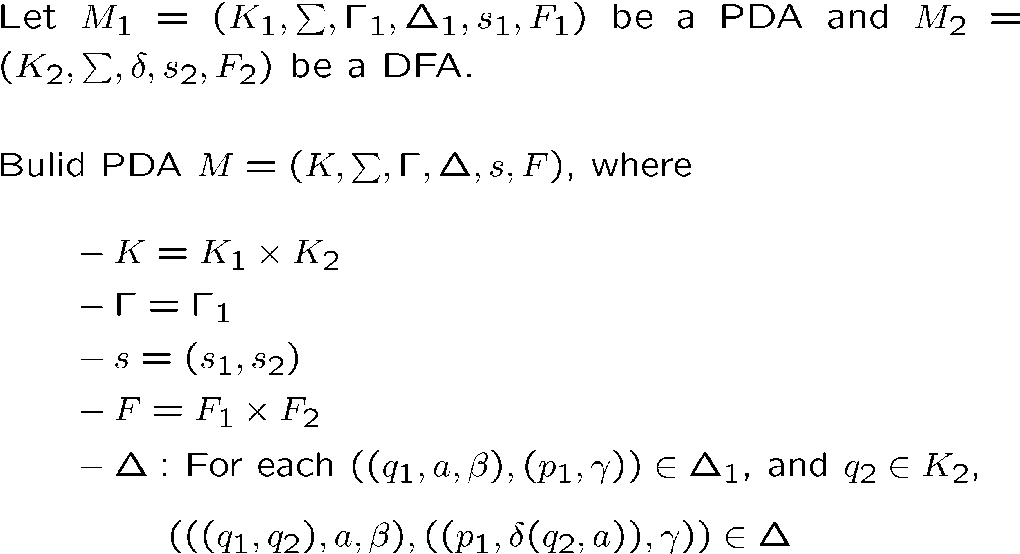
image-20241125161038229

Pumping Theorem for CFL

image-20241231151421837

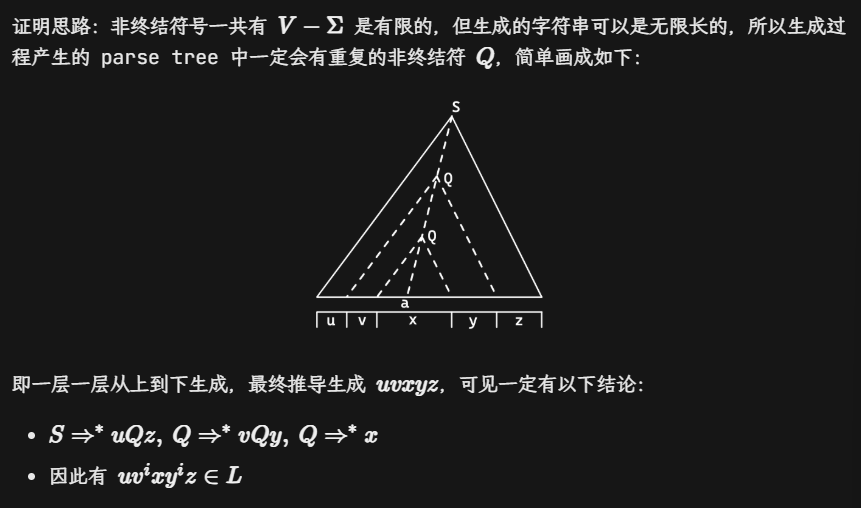
image-20241231151430709

判断某个字符串是否属于某个 CFG

CFG 和 PDA 的相互转化，以及判断字符串是否属于某个 CFG，都有多项式时间内的算法

不存在判断两个 CFG 是否等价的算法，我们从 CFG 生成的 PDA 是不确定性的

采用动态规划的方法

image-20241130110235765

image-20241130110239169