Skip to content

Numerical Functions

:material-circle-edit-outline: 约 491 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

basic functions & operations

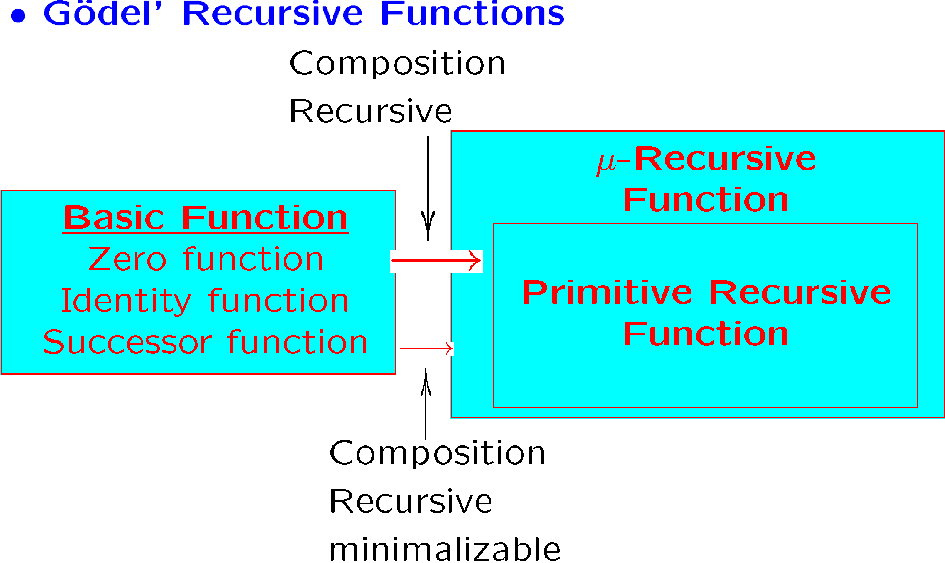
原始递归函数类似 FA，可以从基本函数组合得到

有三个 basic functions：projection functions, zero function, successor funciotn

image-20241215134559303

identity function 是恒等函数，也就是投影函数，从 \(k\) 个元素值选取出某一个元素

还有两个基本运算：composition 和 recurse

image-20241215135117212

primitive recursive functions

我们定义原始递归函数是通过基本函数通过连续的拼接、递归操作得到的函数：

证明一个函数是原始递归的

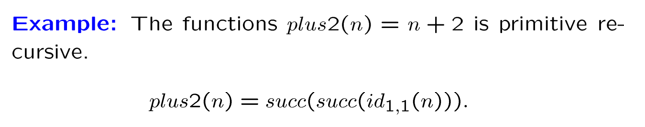
image-20241215135333378

image-20241215140240216

primitive recursive predicate

原始递归谓词指只输出 0 或 1 的函数，也就是一些做判断的函数

image-20241215135931545

常见的原始递归函数

加、乘、幂函数是原始递归的

image-20241215135327806

常量函数是原始递归的

image-20241215135347707

非负数取值函数是原始递归的

image-20241215135403837

除法、取余是原始递归的

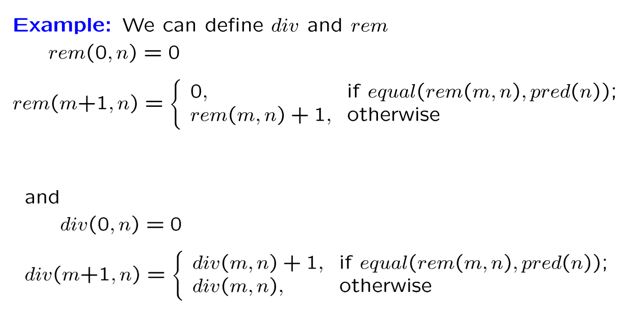
image-20241215140311909

不知道什么函数是原始递归的

image-20241215140621644

求和函数是原始递归的

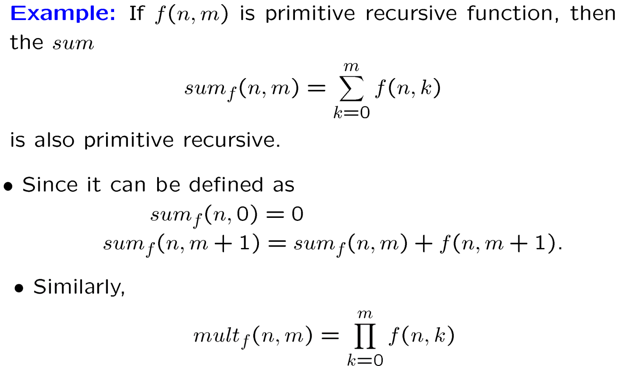
image-20241215140701124

Minimalization 极小化

我们定义一个函数的极小化如下

image-20241221103633375

原函数的极小化函数的值为：

  • 如果存在一个常数 m，将原函数最后一个参数设置为 m，无论其它参数怎么改变，函数的值都为 1
    • 这前面 k 个参数带入极小化函数的结果就是最小的那个满足条件的 m
  • 如果找不到这个 m，结果就为 0

对于任意前 \(k\) 给参数，都能找到一个这样的 m，那么原函数就是可极小化的

\(\mu\) -rec.

一个函数是 \(\mu\) 递归的，如果这个函数可以从基本函数出发，经过 组合、递归、可极小化函数的极小化 三种操作得到

image-20241221105011054

image-20241221105217208

向上的箭头可以看成(m+2)^p

\(\mu\) -rec. 就是递归的

因为产生 \(\mu\) 递归的三种操作都可以分别用图灵机表示出来，所以可以设计出对应的图灵机

反过来的证明见 PPT 105 页，了解即可

image-20241221111543510